7.3. Mono-energetic Particle Beams¶
- class cherab.core.beam.node.Beam¶
A scene-graph object representing a Gaussian mono-energetic beam.
The Cherab beam object holds all the properties and state of a mono-energetic particle beam to which beam attenuation and emission models may be attached. The Beam object is defined in terms of its power, energy, geometric properties and the plasma it interacts with.
The Beam object is a Raysect scene-graph node and lives in it’s own coordinate space. This coordinate space is defined relative to it’s parent scene-graph object by an AffineTransform. The beam parameters are defined in the Beam object coordinate space. Models using the beam object must convert any spatial coordinates into beam space before requesting values from the Beam object. The Beam axis is defined to lie along the positive z-axis with its origin at the origin of the local coordinate system.
While a Beam object can be used to simply hold and sample beam properties, it can also be used as an emitter in Raysect scenes by attaching emission models. The Beam’s bounding geometry is automatically defined from the Beam’s initial width and divergence. The length of the Beam geometry needs to be set by the user.
Beam emission models may be attached to the beam object by either setting the full list of models or adding to the list of models. See the Beam’s ModelManager for more information. The beam emission models must be derived from the BeamModel base class.
Any change to the beam object properties and models will result in a automatic notification being sent to objects that register with the Beam objects’ Notifier. All Cherab models and associated scene-graph objects automatically handle the notifications internally to clear cached data. If you need to keep track of beam changes in your own classes, a callback can be registered with the beam Notifier which will be called in the event of a change to the Beam object. See the Notifier documentation.
Warning
In the current implementation of the Beam class, the Beam can only be associated with a single plasma instance. If your scene has overlapping plasmas the beam attenuation will only be calculated for the plasma instance to which this beam is attached.
- Parameters:
parent (Node) – The parent node in the Raysect scene-graph. See the Raysect documentation for more guidance.
transform (AffineMatrix3D) – The transform defining the spatial position and orientation of this beam. See the Raysect documentation if you need guidance on how to use AffineMatrix3D transforms.
name (str) – The name for this beam object.
- Variables:
atomic_data (AtomicData) – The atomic data provider class for this beam. All beam emission and attenuation rates will be calculated from the same provider.
attenuator (BeamAttenuator) – The method used for calculating the attenuation of this beam into the plasma. Defaults to a SingleRayAttenuator().
divergence_x (float) – The beam profile divergence in the x dimension in beam coordinates (degrees).
divergence_y (float) – The beam profile divergence in the y dimension in beam coordinates (degrees).
element (Element) – The element of which this beam is composed.
energy (float) – The beam energy in eV/amu.
integrator (VolumeIntegrator) – The configurable method for doing volumetric integration through the beam along a Ray’s path. Defaults to a numerical integrator with 1mm step size, NumericalIntegrator(step=0.001).
length (float) – The approximate length of this beam from source to extinction in the plasma. This is used for setting the bounding geometry over which calculations will occur. Units of m.
models (ModelManager) – The manager class that sets and provides access to the emission models for this beam.
plasma (Plasma) – The plasma instance with which this beam interacts.
power (float) – The total beam power in W.
sigma (float) – The Gaussian beam width at the origin in m.
temperature (float) – The broadening of the beam (eV).
>>> # This example shows how to initialise and populate a basic beam >>> >>> from raysect.core.math import Vector3D, translate, rotate >>> from raysect.optical import World >>> >>> from cherab.core.atomic import carbon, deuterium, Line >>> from cherab.core.model import BeamCXLine >>> from cherab.openadas import OpenADAS >>> >>> >>> world = World() >>> >>> beam = Beam(parent=world, transform=translate(1.0, 0.0, 0) * rotate(90, 0, 0)) >>> beam.plasma = plasma # put your plasma object here >>> beam.atomic_data = OpenADAS() >>> beam.energy = 60000 >>> beam.power = 1e4 >>> beam.element = deuterium >>> beam.sigma = 0.025 >>> beam.divergence_x = 0.5 >>> beam.divergence_y = 0.5 >>> beam.length = 3.0 >>> beam.models = [BeamCXLine(Line(carbon, 5, (8, 7)))] >>> beam.integrator.step = 0.001 >>> beam.integrator.min_samples = 5
- density(x, y, z)¶
Returns the bean density at the specified position in beam coordinates.
Note: this function is only defined over the domain 0 < z < beam_length. Outside of this range the density is clamped to zero.
- Parameters:
x – x coordinate in meters.
y – y coordinate in meters.
z – z coordinate in meters.
- Returns:
Beam density in m^-3
- direction(x, y, z)¶
Calculates the beam direction vector at a point in beam coordinate space.
The beam direction (non-normalised) is calculated as follows (z > 0):
\[ \begin{align}\begin{aligned}e_x = x\frac{(ztg(\alpha_x))^2}{\sigma^2 + (ztg(\alpha_x))^2},\\e_y = y\frac{(ztg(\alpha_y))^2}{\sigma^2 + (ztg(\alpha_y))^2},\\e_z = z,\end{aligned}\end{align} \]where \(\sigma\) is the Gaussian beam deviation at origin, \(\alpha_x\) and \(\alpha_y\) are the beam divergence angles in the x and y dimensions respectively.
For z <= 0 the beam direction is (0, 0, 1).
The function returns normalised beam direction.
Note the values of the beam outside of the beam envelope should be treated with caution.
- Parameters:
x – x coordinate in meters.
y – y coordinate in meters.
z – z coordinate in meters.
- Returns:
Direction vector.
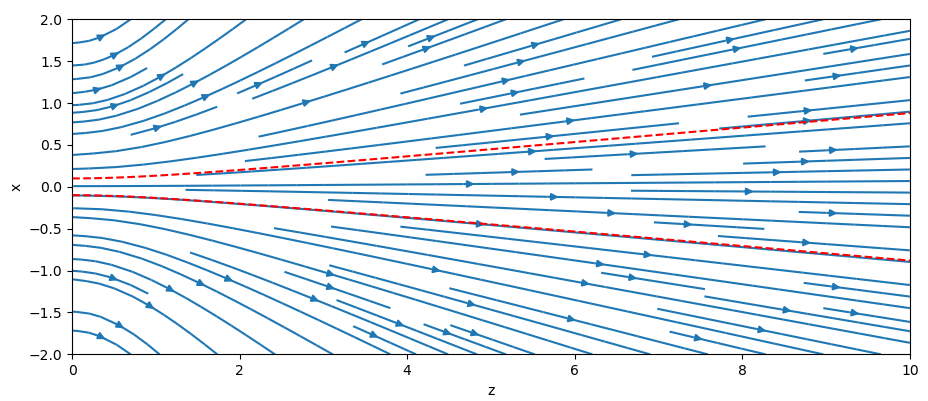
The beam direction pattern in XZ-plane for the beam with sigma = 0.1 m
and divergence_x = 5 \(^{\circ}\).¶